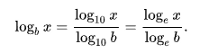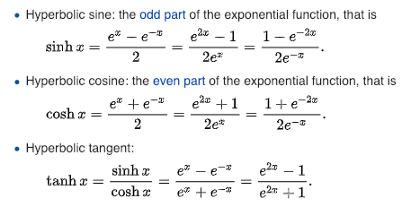STM32 Blue Pill – Shrink your math libraries with Qfplib
Check out this magic trick… Why does Blue Pill think that 123 times 456 is 123,456 ???!!! Here’s the full source code.
Blue Pill thinks that 123 times 456 is 123,456
This article explains how we hacked Blue Pill to create this interesting behaviour, and how we may exploit this hack to cut down the size of our math libraries…
- What are Math Libraries? How does Blue Pill perform math computations?
- Qfplib the tiny math library
- Single vs Double-Precision numbers. Do we really need Double-Precision?
- Filling in the
missing math functions with
nano-float - Testing Qfplib and nano-float
- My experience with Qfplib and nano-float
This article covers experimental topics that have not been tested in production systems, so be very careful if you decide to use any tips from this article.
What are Math Libraries? Why so huge?
If you have used math functions
like sin(), log(), floor(), ... then you would have used the
libm.a
Standard Math Library for C. It’s a bunch of common math functions that we may call from C
and C++ programs running on Blue Pill and virtually any microcontroller and any device.
But there’s a catch… The math functions will perform better on some microcontrollers and devices — those that support hardware floating-point operations in their processors.
Unfortunately Blue Pill is not in that list. The math libraries are implemented in
software, not hardware. So a single call to sin() could actually
keep the Blue Pill busy for a (short) while because of the complicated library code. And
the complicated math code also causes Blue Pill programs to bloat beyond their ROM limit (64 KB).
Is there a better way to do math on Blue Pill? The secret lies in the Magic Trick…
Magic Trick Revealed
Remember the above code from the Magic Trick… Why does Blue Pill think that 123 times 456 is 123,456? Let’s look at the Assembly Code (check my previous article for the “Disassemble” task)…
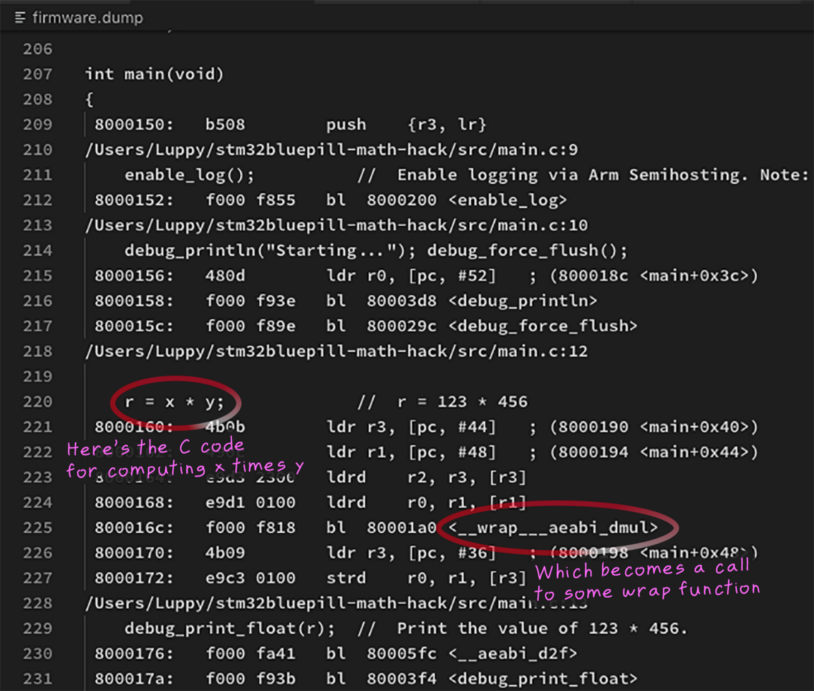
Assembly Code for the magic trick. From https://github.com/lupyuen/stm32bluepill-math-hack/blob/master/firmware.dump
Something suspicious is happening here… the line
r = x * y
has actually been compiled into a function call that looks like…
r = __wrap___aeabi_dmul(x, y)
Multiplication of numbers looks
simple and harmless when we write it as x * y. But remember that x and y are floating-point
numbers. And Blue Pill can’t compute floating-point numbers in hardware. So Blue
Pill needs to call a math library function __wrap___aeabi_dmul to compute x * y !
It looks more sinister now…
Remember this function that appears at the end of the magic trick?
double __wrap___aeabi_dmul(double x, double y) {
return 123456;
}
That’s where the magic happens —
it returns 123456 for any
multiplication of doubles in the program. We have
intercepted the multiplication operation to return a hacked result.
__wrap___aeabi_dmul is typically a function with lots of computation
code inside… 1 KB of compiled code. So our code size will bloat
significantly once we start using floating-point computation on Blue Pill.
Now what if we do this…
double __wrap___aeabi_dmul(double x, double y) {
return qfp_fmul(x, y);
}
What if we
could find a tiny function qfp_fmul that
multiplies floating-point numbers without bloating the code size? That would be perfect for
Blue Pill! qfp_fmul actually exists and it’s part of the Qfplib library, coming up next…
💎 About the
wrap: Thewrapprefix was inserted because we used this linker option in platformio.ini:-Wl,-wrap,__aeabi_dmul. Withoutwrap, the function name is actually__aeabi_dmul. By usingwrapwe can easily identify the functions that we have intercepted. Check this doc for more info on AEABI functions.
Qfplib the tiny floating-point library
Qfplib is a floating-point math library by Dr Mark Owen that’s incredibly small. In a mere 1,224 bytes we get Assembly Code functions (specific to Arm Cortex-M0 and above) that compute…
qfp_fadd, qfp_fsub, qfp_fmul, qfp_fdiv_fast: Floating-point addition, subtraction, multiplication, divisionqfp_fsin, qfp_fcos, qfp_ftan, qfp_fatan2: sine, cosine, tangent, inverse tangentqfp_fexp, qfp_fln: Natural exponential, logarithmqfp_fsqrt_fast, qfp_fcmp: Square root, comparison of floats
Plus conversion functions for integers, fixed-point and floating-point numbers. What a gem!
With Qfplib we may now intercept
any floating-point operation (using the __wrap___aeabi_dmul
method above) and substitute a smaller, optimised version of the
computation code.
Be careful: There are limitations in the Qfplib functions, as described here. And Qfplib only handles single-precision math, not double-precision. More about this…
Single vs Double-Precision Floating-Point Numbers
You should have seen
single-precision (float) and double-precision (double) numbers in C programs…
float x = 123.456; // Single precision (32 bits)
double y = 123.456789012345; // Double precision (64 bits)
Double-precision numbers are more precise in representing floating-point numbers because they have twice the number of bits (64 bits) compared with single-precision numbers (32 bits).
To be more specific…
single-precision numbers are stored in the IEEE 754 Single-Precision
format which gives us 6 significant decimal digits. So this float value is OK because it’s only 6 decimal digits…
float x = 123.456; // OK for Single Precision
But we may lose the seventh digit
in this float value because 32 bits can’t fully accommodate 7
decimal digits…
float y = 123.4567; // Last digit may be truncated for Single Precision
And Blue Pill may think that
x has the same value as y.
We wouldn’t use float to count 10 million dollars (7 decimal
digits or more).
With double-precision numbers (stored as IEEE 754 Double-Precision format) we have room for 15 significant decimal digits…
double y = 123.456789012345; // OK for Double Precision
Double precision is indeed more precise than single precision. BUT…
doublestake up twice the storagedoublesalso require more processor time to compute
This causes problems for
constrained microcontrollers like Blue Pill. Also if we use common math functions like sin(), log(), floor(), … we will actually introduce doubles into our code because the common math functions are declared
as double. (The single-precision equivalent functions are
available, but we need to consciously select them as sinf(), logf(), floorf(), …)
Do we really need Double Precision numbers?
I teach IoT. When my students measure ambient temperature with a long string of digits like 28.12345, I’m pretty sure they’re not doing it right.
Sensors are inherently noisy so I won’t trust them to produce such precise double-precision numbers. Instead I would use a Time Series Database to aggregate sensor values (single-precision) over time and compute an aggregated sensor value (say, moving average for the past minute) that’s more resistant to sensor noise.
If you’re doing Scientific
Computing, then doubles are for you. Then again you probably
won’t be using a lower-class microcontroller like Blue Pill. It’s my hunch that most Blue Pill
programmers will be perfectly happy with floats instead of doubles (though I have no proof).
Always exercise caution when
using floats instead of doubles. There’s a possibility that some intermediate computation will overflow the 6-digit limitation of floats, like this computation. GPS
coordinates (latitude, longitude) may require doubles as well.

nano-float function derived from Qfplib and the unit test cases below. From https://github.com/lupyuen/codal-libopencm3/blob/master/lib/nano-float/src/functions.c#L555-L585
Complete Math Library: nano-float

Functions provided by qfplib
Qfplib provides the basic
float-point math functions. Many other math functions are missing: sinh, asinh, … Can we synthesise the other math functions?
Yes we can! And here’s the proof…
https://github.com/lupyuen/codal-libopencm3/blob/master/lib/nano-float/src/functions.c
nano-float is a thin layer of code I
wrote (not 100% tested) that fills in the remaining math functions by calling Qfplib. nano-float is a drop-in replacement for the standard math library,
so the function signatures for the math functions are the same… just link your program with nano-float instead of the default math library, no recompilation
needed.
This looks like a math textbook exercise but let’s derive the missing functions based on Qfplib…
1️⃣ log2 and log10
were derived from Qfplib’s qfp_fln (natural logarithm function)
because…
2️⃣ asin and acos
(inverse sine / cosine) were derived from Qfplib’s qfp_fsqrt_fast (square root) and qfp_fatan2 (inverse tangent) because…
3️⃣ sinh, cosh and tanh
(hyperbolic sine / cosine / tangent) were derived from Qfplib’s qfp_fexp (natural exponential) because…
4️⃣ asinh, acosh and atanh
(inverse hyperbolic sine / cosine / tangent) were derived from qfplib’s qfp_fln (natural
logarithm) and qfp_fsqrt_fast (square root) because…
So you can see that it’s indeed
possible for nano-float to fill in the missing math functions by
simply calling Qfplib!
But watch
out for Boundary Conditions — the code in nano-float
may not cover all of the special cases like 0, +infinity, -infinity, NaN (not a number), …
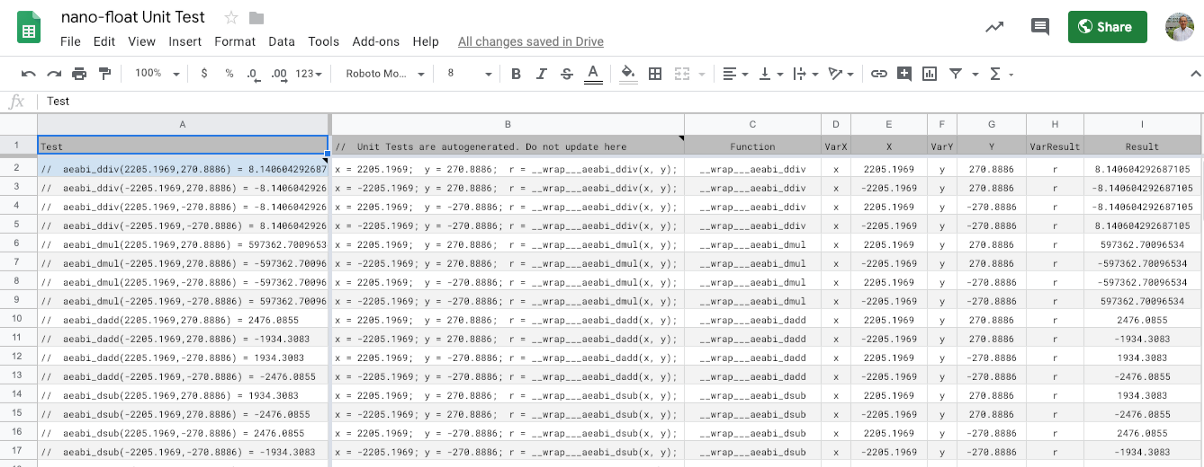
nano-float unit tests automatically extracted from the nano-float source code. From https://docs.google.com/spreadsheets/d/1Uogm7SpgWVA4AiP6gqFkluaozFtlaEGMc4K2Mbfee7U/edit#gid=1740497564
Unit Test with Qemu Blue Pill Emulator
Replacing the standard math
library by nano-float is an onerous tasks. How can we really be
sure that the above formulae were correctly programmed? And that the
nano-float computation results (single precision) won’t deviate too drastically from the original math functions (double
precision)?
It’s not a perfect solution but
we have Unit Tests for nano-float: https://github.com/lupyuen/codal-libopencm3/blob/master/lib/nano-float/test/test.c
These test cases are meant to be
run again and again to verify that the results are identical whenever we make changes to the code. The
test cases were automatically extracted from the nano-float
source code by this Google Sheets spreadsheet…
Unit tests are also meant to be run automatically at every rebuild. But the code requires a Blue Pill to execute. The solution: Use the Qemu Blue Pill Emulator to execute the test cases, by simulating a Blue Pill in software.
So far the test cases confirm that Qfplib is accurate up to 6 decimal digits, when compared with the standard math library (double-precision). Which sounds right because Qfplib uses single-precision math (accurate to 6 decimal digits).
We’ll cover Blue Pill Unit Testing and Blue Pill Emulation in the next article.
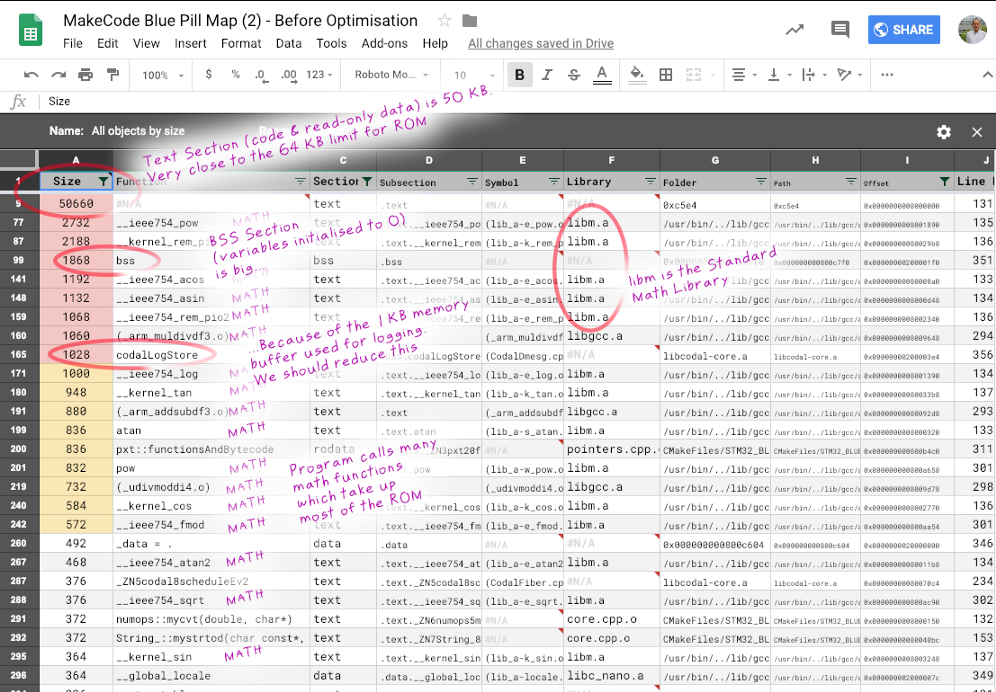
Memory usage of the MakeCode application on Blue Pill, without Qfplib and nano-float. From https://docs.google.com/spreadsheets/d/1DWFoh0Ui9j294htHzQrH-s6MuPRXct2zN8M9pj53CBk/edit#gid=381366828&fvid=1359565135
How I used Qfplib and nano-float
MakeCode is visual programming tool for creating embedded programs for microcontrollers (like the BBC micro:bit), simply by dragging and dropping code blocks in a web browser. It’s the perfect way to teach embedded programming to beginners.
While porting MakeCode to Blue Pill, I had trouble squeezing all the code into Blue Pill’s 64 KB ROM. (The BBC micro:bit has 256 KB of ROM, with plenty of room for large libraries.) After compiling for Blue Pill, I noticed that the math libraries were taking huge chunks of ROM storage (roughly 17 KB), which you can see in the spreadsheet above. So I made these changes…
- Using
__wrap___aeabi_dmulmethod described earlier, I intercepted the single-precision and double-precision comparison and arithmetic operations (multiply, divide) and used Qfplib instead. Here’s the complete list of intercepted functions. - I used
nano-floatas a drop-in replacement for the standard math librarylibm.a. So all calls to common math functions likesin(), log(), floor(), … were handled bynano-float.
After optimisation, the ROM usage has dropped drastically, as shown below. So MakeCode might actually run on Blue Pill, assuming we don’t need double-precision math. I haven’t completed my testing of MakeCode on Blue Pill yet — I’m taking a break from the coding and testing to document my MakeCode porting experience, which is what you’re reading now (and more to come).
Read about Blue Pill memory optimisation in my previous article.
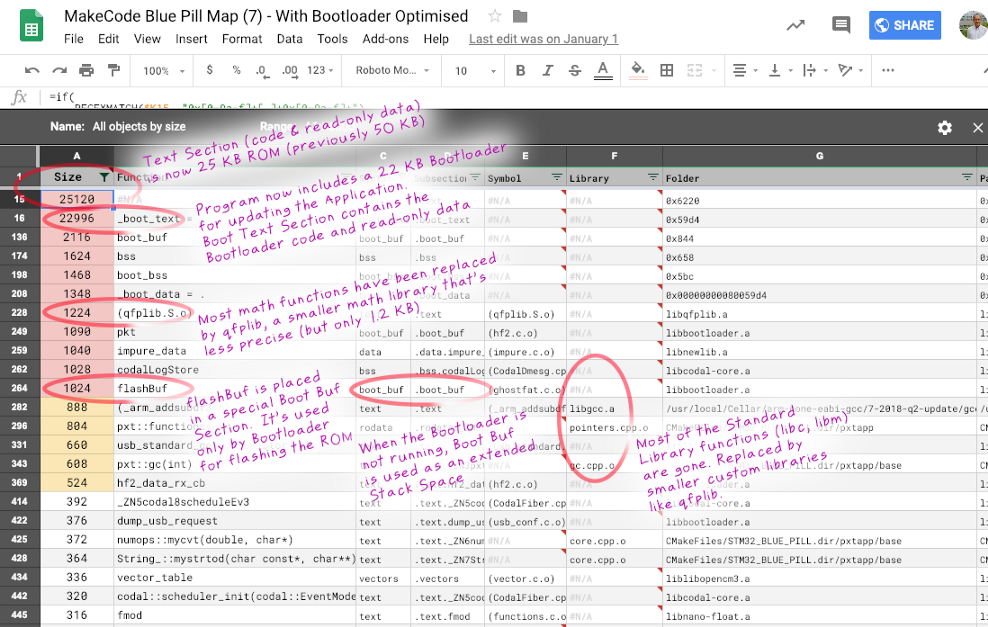
Memory usage of the MakeCode application on Blue Pill, with Qfplib and nano-float. From https://docs.google.com/spreadsheets/d/1OmD1XmUQJTIiXklYx-eui27MFBBhnXrCNaJwSUFDiN8/edit#gid=381366828&fvid=1359565135
The Daring Proposition
In this article I have argued that we don’t need highly-precise double-precision math libraries all the time. It’s plausible that single-precision math (optimised with Qfplib) is sufficient for IoT and for Blue Pill embedded programs. If we accept this, then the lowly Blue Pill microcontroller will be able to run math programs that were previously too big to fit on Blue Pill. Like the MakeCode visual programming tool.
But this needs to be validated through real-world testing (I’ll be validating shortly through MakeCode). For the daring embedded programmers… All the code you need is already in this article, so go ahead and try it out!
Many thanks to Fabien Petitgrand for the precious feedback